Teematietoa
KALENTERIJÄRJESTELMÄ:
HYVÄSTIT DESIMAALIJÄRJESTELMÄLLE
Sinut kutsutaan syntymäpäiväjuhliin 15. syyskuuta klo 20.00. Helppo juttu: merkintä kalenteriin – sieltä näet, että päivä on lauantai – ja sinun tarvitsee tuona juhlapäivänä vain vilkaista kelloa ollaksesi ajoissa. Niin yksinkertaista kellonajan ja päivämäärän sopiminen nykyään on.
Ajassa pysyminen ei ollut ennen niin yksinkertaista, silloin kun ei ollut tarkkoja kelloja eikä päivämääräkään ollut niin helposti tarkistettavissa. Tästä syystä ihminen alkoi jo varhain kehittää kalenterijärjestelmiä ja ajan yksiköitä. Nykyisin käytössä olevat ajan yksiköt eivät ole muualla niin yleisen kymmenjärjestelmän mukaisia – tunti kun on 60 minuuttia, päivä 24 tuntia, viikko seitsemän päivää ja yksi vuosi 365 päivää. Tämä johtuu osittain astronomisista tekijöistä, mutta paljolti myös historiallisista syistä. Kalenterin historiasta löytyy matematiikan opetukseen erilaisia kiehtovia teemoja, joissa etusijalla on omien laskentamenetelmien kehittäminen. Matemaattisesti katsoen niissä on olennaista kokonaisluvuilla ja jäännöksillä laskeminen.
KALENTERI VIE MEIDÄT MUINAISEEN ROOMAAN
Sanan ’kalenteri’ alkuperä löytyy tutkimalla päivämäärän määrittämisen historiaa. Kalenteri juontaa juurensa latinan sanasta ’Kalendae’, jolla antiikin Roomassa viitattiin niihin päiviin, jotka aloittivat kuukauden. Alunperin nämä päivät olivat uudenkuun jälkeisiä päiviä, joita pidettiin juhlapäivinä. Pappi tapasi kutsua kuun jumalatarta Juno Covellaa sanoin „Te calo Iuno Covella!“ (´Kutsun sinua, Juno Covella“) – ja tästä syntyi ‘kalendae‘, ja myöhemmin myös suomen kielen sana ’kalenteri’. Roomalaista elämänmenoa jäsensivät myös kalenterissa käytössä olleet kuukausittaiset nonae- (kuukauden 5. tai 7. päivä) ja idus-päivät (13. tai 15.).
Alkuperäisen roomalaisen kalenterin ongelma oli se, että se perustui kuunkierron vaiheisiin. Vuosi oli täten vain 355 päivän pituinen. Jotta kalenteri olisi myös vuodenaikojen vaihtelun mukainen, lisättiin siihen joka toinen vuosi kokonainen ”karkauskuukausi” (epakt), joka oli 22 tai 23 päivän pituinen. Tämä oli aika sekava järjestelmä. Samaan aikaan käytössä ollut vanha egyptiläinen kalenteri, jossa vuoden pituus oli 365 päivää, vastasi paljon paremmin täyttä aurinkovuotta.
Tuodakseen järjestystä tähän aikakaaokseen Julius Caesar uudisti olennaisesti kalenteria 45 eKr. Tuolloin joihinkin kuukausiin, jotka tuolloin olivat 29 tai 30 päivän mittaisia, lisättiin päiviä, jolloin nykyiset kuukaudet saivat nykyään tunnetut pituutensa – juliaaninen kalenteri oli syntynyt. Helmikuu, joka oli tuolloisen vuoden viimeinen kuukausi, säilytti 28-päiväisenä alkuperäisen pituutensa, koska aikaisempien kuukausien pidennys nosti vuoden pituuden 365 päivään. Joka neljäs vuosi helmikuun loppuun lisätään yksi päivä (karkauspäivä). Caesarin kalenteri oli jo hyvin lähellä nykyisin käytössä olevaa.
Juliaaninen kalenteri nimettiin tietenkin itsensä Julius Caesarin mukaan. Lisäksi silloisen kalenterin viidennen kuukauden nimi ”Quintilis” vaihdettiin Caesarin kunniaksi nimeen ”Iulius” (en ’July’, heinäkuu). Vuonna 186 jKr keisari Augustus noudatti Caesarin esimerkkiä ja vaihtoi silloisen kuudennen kuukauden ”Sextilis” nimeksi ”Augustus” (en ’August’, elokuu).
Tehtävävinkkejä
Kehitä yhdessä oppilaiden kanssa karkaus- tai tasauspäiväkaava. Laskennan perustana voidaan käyttää ns. trooppista vuotta, eli ajanjaksoa, jonka pituus on esim. kevätpäiväntasauksesta seuraavaan kevätpäiväntasaukseen. Trooppisen vuoden, joka on aurinkovuoden tieteellinen nimi, todellinen pituus vaihtelee hieman, mutta sen voidaan tässä katsoa olevan 365,24219 päivää.
- Kuinka paljon trooppinen vuosi on pitempi kuin 365 päivää? Anna vastaus tunteina, minuutteina ja sekunteina.
- Kuinka tarkka juliaanisen kalenterin karkauspäiväsääntö oli? Kuinka monen vuoden kuluttua juliaaninen kalenteri eroaa kokonaisen vuorokauden verran trooppisesta vuodesta?
- Millainen voisi olla sellainen karkaus- tai tasaussääntö, joka olisi pätevä vielä useamman vuosisadan kuluttua?
PÄÄSIÄISEN PÄIVÄMÄÄRÄ:
PAAVI GREGORIUS XIII UUDISTI
KALENTERIN
Juliaaninen kalenteri on pohjimmiltaan käyttökelpoinen vielä nykyäänkin. Sen tasaussääntö aiheutti kuitenkin hankaluuksia. Vuosisatojen kuluessa päivämäärä siirtyi aina vaan kauemmas astronomisesta päivämäärästä, minkä takia esimerkiksi pääsiäisen ajankohdan laskeminen ei enää onnistunut. Kristittyjen suurimman juhlan tulee olla ensimmäisenä sunnuntaina kevätpäiväntasauksen täydenkuun taikka 21. maaliskuun jälkeen. Tämän kirkon näkökulmasta merkittävän puutteen korjaamiseksi matemaatikko Christopher Clavius suunnitteli paavi Gregor XIII:n käskystä 1500-luvulla kalenterireformin. Gregoriaaninen kalenteri otettiin käyttöön vuonna 1582, jolloin siirryttiin 4. lokakuusta suoraan 15. lokakuuhun - jätettiin siis kymmenen päivää pois - Caesarin ajoilta peräisin olevan poikkeaman korjaamiseksi.
Clavius säilytti Caesarin tasaussäännön pääosiltaan – yksi lisäpäivä joka neljäs vuosi – mutta ennakoi myös kolme poikkeusta 400 vuoden ajanjaksolle: Vuodet, joiden vuosiluku on jaettavissa neljällä mutta ei 100:lla, ovat karkausvuosia. Jos vuosiluku on kuitenkin jaollinen 400:lla, on tällöin karkausvuosi.
Tehtävävinkkejä
Laske nykyisin käytössä olevan tasaussäännön tarkkuus: Monenko vuoden kuluttua gregoriaanisen kalenterin käyttöönotosta voidaan suositella karkauspäivän jättämistä pois, jotta kalenteri olisi jälleen aurinkovuoden mukainen?
LASKENTA: PÄÄSIÄISEN PÄIVÄMÄÄRÄN
LASKENTATAPOJA
Paavi Gregoriuksen kalenteriuudistus mahdollisti pääsiäispäivän määrittämisen täsmällisesti. Pääsiäisen ajankohdan laskemisesta tuli kuitenkin jonkin verran monimutkaisempaa. Jo juliaanisen kalenterin aikoihin oli olemassa erityinen laskennan ala kirkollisten juhlapäivien laskemiseksi, jota kutsuttiin latinaksi nimellä ”Computus” (= ’laskenta’). Tämän kalenterilaskennan osaajat olivat kehittäneet vuosien kuluessa systemaattisen menetelmän, jolla pääsiäisen päivämäärä voitiin laskea taulukoiden ja tiettyjen operandien avulla. Gregoriaanisen kalenterin käyttöönoton jälkeen heillä oli runsaasti töitä, sillä vuonna 1852 pois jätetyt kymmenen lokakuun päivää ja uudet tasaussäännöt vaativat uudenlaisia laskutoimituksia. Vuositaulukoita käytettiin pitkään pääsiäisen ajankohdan laskennan perustana. Vasta vuonna 1800 saksalainen matemaatikko Carl Friedrich Gauß onnistui kehittämään joukon yksinkertaisia yhtälöitä, joilla pääsiäissunnuntain ajankohta voitiin määritellä puhtaan laskennallisesti.
Tehtävävinkkejä
Alla oppilaille tehtäväksi kehittää muutamia tapoja pääsiäisen ajankohdan määrittämiseksi! Mikä on pääsiäisen päivämäärä esimerkiksi vuonna 2050 tai 3000? Mikä oli pääsiäisen päivämäärä oppilaiden syntymävuonna?
Perustiedot:
- • Pääsiäistä vietetään ensimmäisenä sunnuntaina, joka tulee 21. maaliskuuta seuraavan täysikuun jälkeen. (lisäsääntö: Nikean vuonna 325 pidetyn ensimmäisen kirkolliskokouksen mukaan pääsiäistä tulee viettää viimeistään 25. huhtikuuta, mutta kun laskennallisesti myös 26.4. olisi myös mahdollinen, tässä tapauksessa pääsiäissunnuntaita vietetään viikkoa aikaisemmin, eli 19.4.)
- Tasaussääntö: Vuosina, jotka ovat jaollisia neljällä, mutta eivät 100:lla, ovat karkausvuosia. Mikäli ne ovat kuitenkin jaollisia 400:lla, lisätään niihin karkauspäivä.
- Kuunkierron pituus, eli kun kuu kiertää maapallon ympäri, on 29,53059 päivää
- Aurinkovuoden pituus on 365,24219 päivää
- Pääsiäisssunnuntaita vietettiin 10. helmikuuta vuonna 1583, eli ensimmäisenä vuonna gregoriaanisen kalenterin käyttöönoton jälkeen.
Laskutehtävät ja avainkysymykset:
- Kuinka monen vuoden välein pääsiäinen osuu jälleen samalle päivälle?
- Mihin kalenterilaskijat tarvitsivat „kultaista lukua“?
- Mitä olivat taannoiset karkauskuukaudet (epakt), ja millainen rooli niillä oli kalenterilaskennassa?
- Miten viikonpäivät otetaan laskennassa huomioon?
Gauss esitti 1816 tällaisen lopullisen kaavan pääsiäisen ajankohdan laskemiseksi:
julianinen kalenteri:
N = 6
M = 15
gregoriaaninen:
N = 6 + INT(vuosi/100) - INT(vuosi/400) - 2
M = 15 + INT(vuosi/100) - INT(vuosi/400
- INT((8 * Int(vuosi/100 + 13) / 25)
a = vuosi mod 19
b = vuosi mod 4
c = vuosi mod 7
d = (M + 19a) mod 30
e = (2b + 4c + 6d + N) mod 7
kun (d + e == 35), siitä seuraa, että: (d + e = 28)
kun (d == 28) ja (e == 6) ja (a > 10), siitä seuraa, että: (d + e = 27)
Pääsiäinen: (22 + d + e) maaliskuuta
(tuloksena voi olla myös päivämäärä, joka sijoittuu huhtikuulle.)
Kaavan tarkempi kuvaus löytyy täältä: http://www.nabkal.de/gauss1.html
ISLAMILAINEN AJANLASKU:
KUUVUODET JA AURINKOVUODET
16. heinäkuuta 622 – tästä päivämäärästä sovittiin 17 vuotta myöhemmin – oli erään toisen kalenterin aloituspäivä, joka on vielä yleisesti käytössä eri puolilla maailmaa. Tuona päivänä profeetta Muhammed, viimeisin islamilainen profeetta, aloitti matkansa Mekasta Medinaan , mitä matkaa kutsutaan nimellä hidschra. Tällä matkalla oli ratkaiseva merkitys islamilaisuuden synnyssä, mistä syystä islamilaisen ajanlaskun alkupäivänä pidetään Muhammedin matkan aloituspäivää.
Kun halutaan laskea tämänhetkinen vuosiluku islamilaisen kalenterin mukaan, on otettava huomioon, että islamilaisuudessa – ainakin uskonnollisissa yhteyksissä – on käytössä kuukalenteri. Arkipäivän asioissa useimmat islamilaiset valtiot noudattavat kuitenkin gregoriaanista kalenteria. Islamilaiset kuukuukaudet alkavat aina „uuden valon hetkestä“, eli siitä, jolloin kuunsirppi uudenkuun jälkeen alkaa jälleen näkyä. Kahdessatoista kuukaudessa on vaihdellen 30 tai 29 päivää, ja karkausvuosien viimeiseen kuukauteen lisätään yksi päivä. 30 vuoden syklin aikana lisätään yksitoista tällaista karkauspäivää, ja tämä tapahtuu joka 2., 5., 7., 10., 13., 16., 18., 21., 24., 26. ja 29. vuosi. Tämänhetkinen 30 vuoden sykli alkoi heinäkuussa 1990, islamilaisen kalenterin vuoden 1411 ensimmäisenä päivänä.
Tehtävävinkkejä
Etsi oppilaittesi kanssa vastaukset seuraaviin kysymyksiin:
- Miten voidaan (suurin piirtein) muuttaa tämänhetkisen gregoriaaninen vuosiluku islamilaiseksi ja päinvastoin?
- Minä vuonna islamilaisen kalenterin vuosiluku ohittaa gregoriaanisen kalenterin vuosiluvun?
- Ylempien luokka-asteiden oppilaat voivat lisäksi yrittää muuttaa jonkin gregoriaanisen kalenterin päivämäärän islamilaiseksi päivämääräksi.
SEITSEMÄN VIIKONPÄIVÄÄ:
MONENLAISIA PULMIA POHDITTAVAKSI
Luku seitsemän on hieman epämukava luku. Alkulukuna sillä on vain kaksi luonnollista jakajaa, ja seitsemällä jaollisuuden tarkistaminen on paljon hankalampaa kuin minkä tahansa muun luvun jaollisuuden tarkistaminen 1:n ja 10:n välillä. Tästä huolimatta juuri seitsemän on arkipäivässämme tärkeä luku, koostuuhan viikko seitsemästä viikonpäivästä, jotka rytmittävät elämäämme. Se, että viikossa on seitsemän päivää, johtuu luultavasti kuunkierron pituudesta. Kuu kiertää kerran maapallon ympäri noin neljän viikon aikana.
Jo antiikin roomalaiset jakoivat viikon seitsemään päivään ja he nimittivät näitä silloin tunnettujen taivaankappaleiden – mm. Auringon ja Kuun – mukaan. Sunnuntai oli nimetty Auringon mukaan, maanantai oli omistettu Kuulle ja tiistai oli Marsin päivä. Keskiviikko oli nimetty Merkuriuksen ja torstai Jupiterin mukaan. Perjantai viittasi Venukseen ja lauantai oli Saturnuksen päivä. Siinä missä saksankielisissä viikonpäivien nimityksissä roomalaiset jumalat joutuivat joidenkin päivien kohdalla antamaan tilaa germaanisille jumalille, englannin ja ranskan kielissä viikonpäivien yhteydet planeettoihin ovat edelleen hyvin nähtävissä: englannin Saturday-sanassa voidaan hyvin nähdä yhteys saturnukseen ja ranskan „vendredi“ viittaa edelleen venukseen.
Seitsemän viikonpäivää tuovat kalenterilaskentaan oman lisähaasteensa. Yhden vuoden päivien lukumäärä ei ole seitsemällä jaollinen, joten jokainen vuosi alkaa eri viikonpäivällä kuin edellinen. Kun halutaan tietää mille viikonpäivälle jokin päivämäärä osuu, tämä voidaan ratkaista laskutoimitusten avulla. Samoin kuin pääsiäissunnuntain laskemisessa, myös tässä on tasaussäännöillä keskeinen rooli.
Tehtävävinkkejä
Laskekaa oppilaiden kanssa minä viikonpäivänä he ovat syntyneet. Millaisia ratkaisutapoja tässä voidaan käyttää? Miten ratkaisumallit voidaan esittää matemaattisesti? Apuna voidaan käyttää seuraavia lähtökohtia:
- ikuisen (tai useamman vuosisadan ajan voimassa olevan) kalenterin luonnos
- päässälaskumenetelmä (esim. doomsday-kaava), jossa laskenta perustuu johonkin tietyyn päivämäärään ja tuolloiseen viikonpäivään
- puhtaan matemaattinen malli, joka on voimassa tietyn ajan (esim. 10, 100 tai 400 vuotta – riippuen sovellettavista tasaus/karkaussäännöstä) tai joka on voimassa gregoriaanisen kalenterin alusta lähtien.
ZELLERIN KONGRUENSSI
Matemaattisia malleja viikonpäivän määrittämiseksi ovat esittäneet saksalainen matemaatikko Gauß ja muutamia vuosia myöhemmin matemaatikko ja teologi Christian Zeller. Erityisesti ns. Zellerin kongruensia käytetään vielä nykyäänkin tietojenkäsittelyssä. Gregoriaaniseen kalenteriin sopiva saava on esitetty tässä:
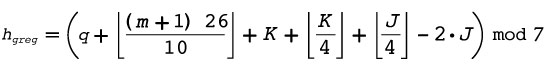
Tässä kaavassa symboli q viittaa päivään ja m kuukauteen (kuukaudet maaliskuusta joulukuuhun on numeroitu 3 - 12, tammikuuhun viitataan edellisvuoden luvulla 13 ja helmikuuhun luvulla 14). J viittaa puolestaan vuosisatoihin (nelinumeroisissa vuosiluvuissa kaksi ensimmäistä numeroa) ja K ilmaisee vuosiluvun kahta viimeistä numeroa. Jos etsitään tammikuun tai helmikuun viikonpäivää, on muistettava käyttää edellisvuoden vuosilukua. Kaava antaa tuloksen h lukuna välillä 0 - 6, joka vastaa viikonpäivää: 0 on lauantai, 1 sunnuntai jne.
PÄÄSSÄLASKIJOILLE:
DOOMSDAY-MENETELMÄ
Brittiläisen John Conwayn vuonna 1970 kehittämän Doomsday-menetelmän lähtökohta on aivan toisen tyyppinen. „Doomsday“ -sanalla tarkoitetaan tässä yhteydessä sitä viikonpäivää, jolle osuu helmikuun viimeinen päivä. Laskennan perustana voidaan käyttää minkä tahansa vuoden helmikuun viimeisen päivän viikonpäivää. Karkausvuosina tämä päivä on 29.2., ja normaalivuosina 28.2. Tästä päivästä on verrattain helppoa johtaa edellisten ja seuraavien päivien, kuukausien ja vuosien viikonpäivät. Seuraavat muistisäännöt helpottavat päässälaskua:
- Jokaisena normaalina vuotena viikonpäivä siirtyy yhden päivän eteenpäin ja karkausvuosina kaksi päivää. Kun 28.2.2010 osuu sunnuntaille, täytyy 28.2.2011 olla maanantai. 2012 on karkausvuosi, mistä johtuen 29.2. „doomsday“ on keskiviikko.
- Päivämäärien 4.4., 6.6., 8.8., 10.10. ja 12.12. viikonpäivä on sama kuin „tuomiopäivän“ (doomsday).
- Sama pätee päivämääriin 5.7., 7.5., 7.11. ja 11.7.
- Normaalivuosina „doomsday“ on 3.1., karkausvuosina 4.1.
Löytävätkö oppilaat muita muistisääntöjä tai säännönmukaisuuksia? Mitkä kuukaudet alkavat samalla viikonpäivällä? Montako päivää tuomiopäivästä on jouluun ja kuinka monta päivää on joulusta tuomiopäivään?
Vinkki opetukseen: perjantai 13.
Perjantaita 13. päivää pidetään epäonnen päivänä. Pyydä oppilaita ottamaan selvää, onko näitä perjantai 13. -päiviä erityisen usein. Minkä ajanjakson pohjalta asiaa tulee tarkastella, jotta kaikki tasaussäännöt tulevat huomioon otetuiksi? Miten voidaan laskea viikonpäivien jakauma tietyn ajanjakson kuluessa?
MAYA-KALENTERI:
TULEEKO MAAILMANLOPPU JOULUKUUSSA?
Kun Saksassa alkoi syksy kalenterin mukaan 22. syyskuuta 2012, vastasi tätä Maya-kalenterissa sen ns. „pitkälaskun“ mukaan päivämäärä 12.19.19.13.10. Tuona päivänä alkoi tämän vanhan keskiamerikkalaisen kalenterin mukaisesti sen pisimmän aikavälin viimeinen jakso: 20. joulukuuta loppui – kalenterin mukaan syksyn loppuessa – Maya-ajanlaskun 13. Baktun-sykli. Baktun-ajanjakso on pisin Mayakalenterin „pitkälaskussa“ käytetty ajan yksikkö. Uusi Baktun-jakso alkaa vain 144 000 päivän välein. Mayojen ennustukset tai mitkään taivaalta luettavissa olevat seikat eivät enteilleet maailmanloppua tämän Baktun-jakson päättyessä.
Päivämäärän merkitsemiseen mayat käyttivät kantalukuesitysmuotoa, jossa jokainen merkkipaikka kuvasi tiettyä aikaväliä.
K’in bezeichnet die kleinste und letzte Stelle und umfasst einen Tag.
20 k’in entsprechen einem uinal.
18 uinal, also 360 Tage, ergeben ein tun.
20 tun, also 7.200 Tage, sind ein k’atun.
20 k’atun wiederum sind 144.000 Tage und damit ein baktun.
Merkintä alkaa Baktun-jaksoista ja seuraavat yksiköt erotetaan pistein. Esimerkiksi meidän kalenterisen syksyn alkupäivämäärä, 22. syyskuuta 2012, merkitään pitkälaskun mukaan 12.19.19.13.10, eli maya-ajanlaskun mukaan: 12 baktun + 19 katun + 19 tun + 13 uinal + 10 kin.
Tehtävävinkkejä
Laske mikä on meidän kalenterimme mukaan mayojen kalenterin ensimmäinen päivä. Miten oppilaiden syntymäpäivät merkittäisiin pitkälaskujärjestelmän mukaisesti? Onko mahdollista kehittää kaava tai kaavoja laskennan helpottamiseksi?
Seuraavassa osoitteessa voit muuntaa gregoriaanisen kalenterin päivämääriä mayakalenterin päivämääriksi: http://www.vinckensteiner.com/kultur/kalender/
KKALENTERIN TODENNÄKÖISYYDET:
SYNTYMÄPÄIVÄPARADOKSI
Palatkaame takaisin nykypäivään! Kuvittele katsovasi jalkapallo-ottelua, jossa kummastakin joukkueesta kentällä on yksitoista pelaajaa ja lisäksi päätuomari. Miten suurella todennäköisyydellä kahdella kentällä olevista 23 henkilöstä on sama syntymäpäivä (syntymävuoden ei tarvitse olla sama)? Vastaus: todennäköisyys 50 prosenttia! Tämä tulos tuntuu useimmista yllättävältä, sillä 23 tuntuu pieneltä luvulta verrattuna 365:een. Tästä syystä tätä todennäköisyyttä kutsutaankin „syntymäpäiväparadoksiksi“. Kalenteri on siis mahdollista liittää myös todennäköisyyksien laskemiseen.
Tehtävävinkkejä
Arvioi oppilaiden kanssa kuinka suurella todennäköisyydellä 23 henkilölle osuu kaksi yhteistä syntymäpäivää ja laatikaa sitten yhdessä malli syntymäpäiväparadoksin laskemiseksi
-
Kuinka monta mahdollisuutta syntymäpäivien jakautumisessa on yhden vuoden eli 365 päivän jaksolle?
Vastaus: 3652 -
Kuinka monta mahdollisuutta syntymäpäivien jakautumisessa on ainoastaan eri päiville vuoden aikana?
Vastaus: 365 * 364 ... (365-(23-1))
Takaisin