TEEMAOSIO
Pilvettömänä yönä tähtitaivasta voi tarkastella loputtomiin. Silloin voi
ymmärtää, kuinka loputtoman suuri maailmankaikkeus on. Yhtäkkiä
maapallo tuntuukin aivan pieneltä, sillä sitä ympäröi tuntematon
avaruus, jonka rajattomuus on vaikea ymmärtää. Monen
vosituhannen ajan tähtitieteilijät eri puolilla maailmaa ovat
yrittäneet paljastaa maailmankaikkeuden salaisuuksia.
Matematiikka on tärkeä elementti tähtitieteessä.
"Luonnon kirja on kirjoitettu matematiikan kielellä",
totesi Galileo Galilei jo vuonna 1623. Toisin sanoen:
Matematiikka mahdollistaa luonnontieteellisten havaintojen
esittämisen lukuina, kaavoina ja malleina, ennustusten
laatimisen ja erilaisten kokeiden suorittamisen. "Matematiikan
avulla tiedemiehet voivat ilmaista, millaista 'tuolla ylhäällä' on tai
miten joku materiaali on rakentunut", kertoo Recklinghausenin
observatorion johtaja, tohtori Burkard Steinrücken. "Teorian avulla
fyysikoiden on mahdollista kehittää kokeita näiden asioiden tutkimiseksi."
Avaruuden ja maailmankaikkeuden herättämää innostusta voidaan hyvin
hyödyntää matematiikan opetuksessa, esimerkiksi siten, että oppilaat saavat
laskea planeettojen kiertoratoja ja esittää maailmankaikkeuden valtavia etäisyyksiä pienemmissä, maapallolla käytetyissä mittakaavoissa.
ymmärtää, kuinka loputtoman suuri maailmankaikkeus on. Yhtäkkiä
maapallo tuntuukin aivan pieneltä, sillä sitä ympäröi tuntematon
avaruus, jonka rajattomuus on vaikea ymmärtää. Monen
vosituhannen ajan tähtitieteilijät eri puolilla maailmaa ovat
yrittäneet paljastaa maailmankaikkeuden salaisuuksia.
Matematiikka on tärkeä elementti tähtitieteessä.
"Luonnon kirja on kirjoitettu matematiikan kielellä",
totesi Galileo Galilei jo vuonna 1623. Toisin sanoen:
Matematiikka mahdollistaa luonnontieteellisten havaintojen
esittämisen lukuina, kaavoina ja malleina, ennustusten
laatimisen ja erilaisten kokeiden suorittamisen. "Matematiikan
avulla tiedemiehet voivat ilmaista, millaista 'tuolla ylhäällä' on tai
miten joku materiaali on rakentunut", kertoo Recklinghausenin
observatorion johtaja, tohtori Burkard Steinrücken. "Teorian avulla
fyysikoiden on mahdollista kehittää kokeita näiden asioiden tutkimiseksi."
Avaruuden ja maailmankaikkeuden herättämää innostusta voidaan hyvin
hyödyntää matematiikan opetuksessa, esimerkiksi siten, että oppilaat saavat
laskea planeettojen kiertoratoja ja esittää maailmankaikkeuden valtavia etäisyyksiä pienemmissä, maapallolla käytetyissä mittakaavoissa.
Astronomia ja astrologia
Vuosisatojen ajan ei tehty tarkkaa eroa taivaan tapahtumien tarkkailun
ja niiden ihmisen kohtaloon liittyvän tulkinnan välillä - monissa
kulttuureissa uskottiin, että planeettojen asemien muutoksista
voitaisiin ennustaa tulevaisuutta. Tähtitieteilijä Johannes Kepler
(1571-1630) laati avaruuteen liittyvien laskelmiensa ohessa
myös horoskooppeja. Käsitys tieteen olemuksesta muuttui
vasta valistuksen aikana: Tuosta ajasta lähtien on ajateltu,
että astronomiassa pyritään kuvaamaan taivaankappaleita
luonnontieteellisellä tavalla ja yritetään selvittää
maailmankaikkeuden lainalaisuuksia. Tähän viittaa myös
nimitys astronomia: Se koostuu kreikan kielen sanoista
ástron (tähti) ja nómos (laki).
Gauss löytää kadonneen planeetan
Seuraavina vuosisatoina astronomia tarjosi - enemmän kuin tänään - hedelmällisen tutkimusalueen tutkijoille, jotka tähtäsivät tieteentekijän maineeseen. Tuolloin ei ollut kovinkaan epätavallista toimia tutkijana yhtä aikaa monella luonnontieteen alueella. Esimerkiksi nykyään ennen muuta matemaatikkona tunnettu Carl-Friedrich Gauss laski vuonna 1801 kiertoradan vastikään löydetylle Ceres-kääpiöplaneetalle. Sattui nimittäin niin, että tähtitieteilijät hukkasivat tämän planeetan 40 päivää sen löytämisen jälkeen. Useat tähtitieteilijät yrittivät turhaan laskea planeetan kiertorataa löytääkseen sen uudelleen taivaalta. He tekivät laskelmissaan seuraavia virheitä: he perustivat laskelmansa ympyrän muotoiseen kiertorataan. Gauss puolestaan oletti kiertoradan olevan elliptinen ja onnistui laskemaan kiertoradan useamman tunnetun planeetan sijaintipisteen pohjalta "pienimmän neliösumman menetelmää" käyttäen. Tästä seurasi se, että tähtitieteilijät onnistuivat löytämään Ceres-planeetan uudelleen joulukuussa 1801. Pienimmän neliösumman menetelmä on vielä tänäänkin käytössä satunnaislaskennassa
Alkuräjähdyksestä maapalloon
Vajaat 14 miljardia vuotta sitten tapahtui jotakin käsittämätöntä: maailmankaikkeutemme syntyi kirjaimellisesti tyhjästä: Avaruus, aika ja materia ovat olleet olemassa tuosta hetkestä lähtien - ainakin useimpien astronomisten teorioiden mukaan. Matka tästä merkittävästä hetkestä maailmankaikkeuteen, jollaisena sen tänään tunnemme, on ollut pitkä. Ensin tuossa syntyvässä tilassa risteili vain joitakin alkeishiukkasia. Ensimmäiset galaksit syntyivät noin 300 miljoonaa vuotta tuon hetken jälkeen. Aurinkokuntamme kehittyi vasta noin 9 miljardin vuoden kuluttua. Vielä 4,7 miljardin vuoden ajan maapallomme kiersi asumattomana auringon ympäri, kunnes lopulta ihminen alkoi kehittyä. Maailmankaikkeuden mittapuun mukaan meidän aikamme maapallolla on kuitenkin lyhyt: Noin 7,5 miljardin vuoden kuluttua, kun aurinko on käyttänyt vetyvarastonsa loppuun, se paisuu "punaiseksi jättiläiseksi" - merkiten elämän loppumista maapallolla. Noin kolmen miljardin vuoden kuluttua tästä aurinko kutistuu "valkoiseksi kääpiötähdeksi".
Projektivinkki
Maailmankaikkeuden ja maapallon syntyyn liittyviä valtavan pitkiä ajanjaksoja on vaikea käsittää. Siirrä oppilaittesi kanssa maailmankaikkeuden historia pienempään mittakaavaan. Olettaen, että miljoona vuotta vastaa yhtä minuuttia, kuinka paljon aikaa kului galaksien syntyy ja ...Lue lisää
Maailmankaikkeuden ja maapallon syntyyn liittyviä valtavan pitkiä ajanjaksoja on vaikea käsittää. Siirrä oppilaittesi kanssa maailmankaikkeuden historia pienempään mittakaavaan. Olettaen, että miljoona vuotta vastaa yhtä minuuttia, kuinka paljon aikaa kului galaksien syntyy ja maapallon syntyyn? Mitä muita "virstanpylväitä" oppilaat voivat tutkia ja laskea maailmankaikkeuden ja maapallon historiassa? Siirrä lopuksi kaikki kehitysvaiheet aikajanalle.
Lue vähemmän
Lue vähemmän
Miten maailmankaikkeus tulee kehittymään?
Alkuräjähdysteoria ei voi yksin selittää sitä, miten maailmankaikkeus kehittyy tästä eteenpäin. Tiedemiehen ovat huomanneet mittailemalla galaksien välisten etäisyyksien etäisyyksiä, että maailmankaikkeus paitsi laajenee, niin myös, että tämä laajeneminen kiihtyy kaiken aikaa. Tämän laajenemisen laskemisessa käytetään niin sanottua Hubblen vakiota 
. Nimitys on peräisin yhdysvaltalaiselta astronomilta Edwin Hubblelta. Hubblen vakion avulla voidaan laskea maailmankaikkeuden ikä. Oikeastaan tässä ei ole kyse vakiosta, sillä Hubblen vakio muuttuu ajan kuluessa. Tämän takia astronomit käyttävät myös nimitystä Hubblen parametri. Hubblen parametrin määrittämiseen säännöllisin väliajoin käytetään eri tähtikaukoputkien tuottamia kuvia. Hubblen parametrin arvo vaihtelee riippuen mittausmenetelmästä. Sen arvo on noin 
.
Mpc (Mpc on lyhenne tähtitieteessä käytetystä Megaparsec-pituusmittayksiköstä).
. Nimitys on peräisin yhdysvaltalaiselta astronomilta Edwin Hubblelta. Hubblen vakion avulla voidaan laskea maailmankaikkeuden ikä. Oikeastaan tässä ei ole kyse vakiosta, sillä Hubblen vakio muuttuu ajan kuluessa. Tämän takia astronomit käyttävät myös nimitystä Hubblen parametri. Hubblen parametrin määrittämiseen säännöllisin väliajoin käytetään eri tähtikaukoputkien tuottamia kuvia. Hubblen parametrin arvo vaihtelee riippuen mittausmenetelmästä. Sen arvo on noin . Mpc (Mpc on lyhenne tähtitieteessä käytetystä Megaparsec-pituusmittayksiköstä).
Onko maapallo maailmankaikkeuden ainoa asuttu planeetta?
Niin sanottujen eksoplaneettojen etsintä ei ole aivan niin kuin spekulaatioon perustuvaa kuin alkuräjähdysteoria, mutta ainakin yhtä jännittävää. Eksoplaneetat kulkevat kiertorataa muiden kuin meidän aurinkomme ympärillä - ja koska ne eivät tuiki kuten tähdet, niitä on vaikea havaita. Ensimmäinen eksoplaneetta löydettiin vuonna 1990, ja nykyään sellaisia tunnetaan yli 700. Erityisen kiinnostavia tutkimuksen kannalta ovat maapallon kaltaiset planeetat, joilla on voinut kehittyä elämää. "Sen mahdollisuus, että eläviä organismeja olisi kehittynyt jossakin päin maailmankaikkeutta, on hyvin suuri", arvioi tähtitornin johtaja Steinrücken. "Vähintään joka toisella tähdellä on planeettajärjestelmä - ja tämän takia on varmasti olemassa myös sellaisia planeettoja, jotka ovat sopivalla etäisyydellä auringostaan, jolloin niillä esiintyy vettä nestemäisessä muodossa." Voiko sitten elämää kehittyä tuollaisissa olosuhteissa, siihen kysymykseen nykytiede ei pysty vastaamaan. "Tunnemme nimittäin vain yhden ainoan planeetan, jolla tämä on tapahtunut, nimittäin oman planeettamme. Tämän ainoan tapauksen perusteella ei voida tilastollisesti tehdä johtopäätöksiä koko maailmankaikkeudesta. Moni seikka viittaa kuitenkin siihen, ettei oma maailmankaikkeutemme ole mitenkään erikoislaatuinen." Vasta joulukuussa 2011 NASA ilmoitti Kepler-22b-eksoplaneetan löydöstä, joka sijaitsee lähimpänä maapalloa. Meidän ei kuitenkaan tarvitse aivan vielä valmistautua kohtaamaan Keplerin asukkaita - maapallolta on nimittäin n. 600 valovuoden matka Kepler-22:n aurinkokuntaan. Jo vuonna 1961 amerikkalainen astrofyysikko Frank Drake esitti matemaattisen arvion siitä, kuinka todennäköistä on, että galaksissamme on muuta älykästä elämää. Drake käytti kaavassaan seitsemää eri tekijää, joihin kuuluivat esimerkiksi uusien tähtien syntymistiheys, eksoplaneettojen lukumäärä ja tietyt tiedot ilmakehästä. Monet näistä tekijöistä tunnetaan kuitenkin vain lähinnä likimääräisinä arvioina. Suomenkieliseltä sivustolta löytyy Draken kaavan esimerkkilaskuri:http://cs.joensuu.fi/~vtenhu/drake.html
Opetusvinkki
Draken kaavan eri tekijät ovat kiinnostavia tutkimuskohteita ja tarjoavat runsaasti aiheita tieteelliselle pohdiskelulle. Kokeile oppilaittesi kanssa Draken kaavaa eri arvoilla ja vertaile tuloksia.
Maailmankaikkeuden etäisyydet ja mittasuhteet
Kuvitellaanpa matka Australiaan: Maapallon mittakaavassa tuo n. 13500 km:n matka on jo melkoisen pitkä. Jos sama matka tehtäisiin suoraan kohti avaruutta, päästäisiin lopulta vain juuri ja juuri eksosfäärin - maapallon ilmakehän etäisimmän kerroksen - ulkolaidalle. Jo yksin kuu on lähimmillään 363300 km:n etäisyydellä maapallosta. Etäisyys kuuhun vastaa noin 27-kertaista matkaa Keski-Euroopasta Australiaan. Nämä etäisyydet ovat kuitenkin vain pieni hyppäys aurinkokuntamme mittakaavassa. Venus, joka on Maata seuraavaksi lähin planeetta, käväisee lähimmillään noin 40 miljoonan kilometrin etäisyydellä Maasta. Mars - seuraavaksi lähin planeetta - ei koskaan tule lähemmäksi kuin 56 miljoonan kilometrin etäisyydelle maapallosta.
Avaruuden ja Maan mittayksiköt
Jo oman aurinkokuntamme etäisyydet osoittavat, että maapalloa yleisesti kuvaavat mittayksiköt ovat liian pieniä maailmankaikkeuden kuvaamiseen. Tähtitieteilijöiden käyttämät mittayksiköt viittaavat kuitenkin usein maapalloon: Usein planeettojen ympärysmitat ja massat ilmoitetaan suhteessa Maan ympärysmittaan ja massaan. Astronominen yksikkö eli tähtitieteellinen yksikkö (lyhenne au, engl. Astronomical Unit) on alkuperäisen määritelmän mukaan Maan keskietäisyys Auringosta, joka on noin 149,6 miljoonaa kilometriä.
Opetusvinkki
Tähtitieteen mittayksiköitä voi hyvin käyttää opetuksessa: Oppilaita voisi esimerkiksi kiinnostaa laskea aurinkokuntamme planeettojen massoja ja ympärysmittoja Maan massoina ja ... Lue lisää
Tähtitieteen mittayksiköitä voi hyvin käyttää opetuksessa: Oppilaita voisi esimerkiksi kiinnostaa laskea aurinkokuntamme planeettojen massoja ja ympärysmittoja Maan massoina ja ympärysmittoina. Mikä planeetta on massaltaan suurin? Millä planeetalla on suurin tiheys? Näissä laskelmissa tarvitaan potensseja ja geometrian taitoja. Aurinkokuntamme planeettojen tiedot:
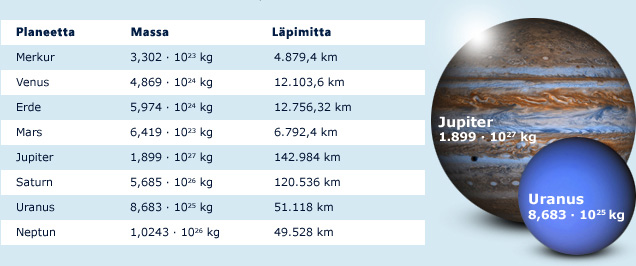
Etäisyydet muuttuvat vieläkin "tähtitieteellisemmiksi", kun siirrymme omasta aurinkokunnastamme tarkastelemaan koko linnunrataamme ja sen välitöntä ympäristöä. Tässä yhteydessä etäisyydet ilmoitetaan usein valovuosina
(9,461
m) ) taikka, erityisesti tieteispiireissä, Parsekeina. Yksi parsek (pc) on noin 3,26 valovuotta. Etäisyys lähimpänä omaa linnunrataamme sijaitsevaan Andromedan galaksiin on noin 2,5 miljoonaa valovuotta tai vajaat 800 kiloparsekia (kpc). Voimme kuitenkin nähdä sen paljain silmin pimeänä kirkkaana yönä Andromedan tähdistössä.
Projektivinkki: Jotta oppilaat oppisivat paremmin ymmärtämään maailmankaikkeuden valtavat etäisyydet, voitte yhdessä rakentaa aurinkokuntamme pienoismallin. Jos Maa olisi tennispallon kokoinen, mikä olisi sen etäisyys auringosta? Mikä tuolloin olisi Jupiterin läpimitta? Näissä tehtävissä tarvitaan monia yläkoulun matematiikantaitoja verrannollisuuksien laskemisesta ja potenssilaskuista kulmiin liittyvään laskentaan. Voi kuitenkin olla, että voitte pian joutua siirtymään luokkahuoneesta käytävälle - nimittäin pienoismallin rakentaminen pienessäkin mittakaavassa vaatii aika paljon tilaa. Lue vähemmän
Etäisyydet muuttuvat vieläkin "tähtitieteellisemmiksi", kun siirrymme omasta aurinkokunnastamme tarkastelemaan koko linnunrataamme ja sen välitöntä ympäristöä. Tässä yhteydessä etäisyydet ilmoitetaan usein valovuosina
(9,461
m) ) taikka, erityisesti tieteispiireissä, Parsekeina. Yksi parsek (pc) on noin 3,26 valovuotta. Etäisyys lähimpänä omaa linnunrataamme sijaitsevaan Andromedan galaksiin on noin 2,5 miljoonaa valovuotta tai vajaat 800 kiloparsekia (kpc). Voimme kuitenkin nähdä sen paljain silmin pimeänä kirkkaana yönä Andromedan tähdistössä.Projektivinkki: Jotta oppilaat oppisivat paremmin ymmärtämään maailmankaikkeuden valtavat etäisyydet, voitte yhdessä rakentaa aurinkokuntamme pienoismallin. Jos Maa olisi tennispallon kokoinen, mikä olisi sen etäisyys auringosta? Mikä tuolloin olisi Jupiterin läpimitta? Näissä tehtävissä tarvitaan monia yläkoulun matematiikantaitoja verrannollisuuksien laskemisesta ja potenssilaskuista kulmiin liittyvään laskentaan. Voi kuitenkin olla, että voitte pian joutua siirtymään luokkahuoneesta käytävälle - nimittäin pienoismallin rakentaminen pienessäkin mittakaavassa vaatii aika paljon tilaa. Lue vähemmän
Opetusvihje - planeettojen kiertoradat
Tähtitaivaan tarkastelu on motivoivaa ja opettavaista. "Monet oppilaat eivät tiedä, että planeettojen liikettä tähtitaivaalla voi seurata paljain silmin", kertoo tohtori Burkard Steinrücken...Lue lisää
Tähtitaivaan tarkastelu on motivoivaa ja opettavaista. "Monet oppilaat eivät tiedä, että planeettojen liikettä tähtitaivaalla voi seurata paljain silmin", kertoo tohtori Burkard Steinrücken Recklinghausenin observatoriosta.
Yksinkertaisilla koulussa tehtävillä kokeilla voidaan valottaa luonnontieteilijöiden työtä ja samalla heittää oppilaille jännittäviä matemaattisia haasteita. "Oppilaat voivat esimerkiksi kehittää mittalaitteen mitatakseen etäisyyksiä jostakin tietystä planeetasta muihin tähtiin. Oppilaat oppivat myös, miten kiertorata muuttuu. Silloin päädytään pohtimaan teoriaa: Miksi planeetalle tapahtuu noin? Onko olemassa geometristä kaavaa kiertoradan laskemiseksi? Yläkoulun viimeisiltä luokilta alkaen voidaan tähtitaivaan tarkkailu yhdistää matematiikkaan planeettojen kiertorataa koskevissa projekteissa. Matemaattisista työkaluista käytetään tässä yhteydessä mm. kartioleikkauksien laskentaa. Keplerin säännöt antavat ideoita ja perustan kiertoratojen laskemiselle.
Vihje: Simuloikaa yhdessä oppilaiden kanssa Auringon, Kuun ja muiden planeettojen liikkeitä. Aurinkoa voi simuloida esim. lampulla ja Kuuta sekä Maata kahdella erisuuruisella pallolla. Mikä näistä taivaankappaleista sijoittuu muiden väliin? Mikä näistä kiertää mitäkin ja kuinka usein? Miltä asetelma näyttää auringon- ja kuunpimennyksen aikaan? Missä kuu sijaitsee uuden kuun aikaan? Tämä koe osoittaa useimmiten, että näissä tutuissakin taivaankappaleissa on paljon opittavaa. Lue vähemmän
Yksinkertaisilla koulussa tehtävillä kokeilla voidaan valottaa luonnontieteilijöiden työtä ja samalla heittää oppilaille jännittäviä matemaattisia haasteita. "Oppilaat voivat esimerkiksi kehittää mittalaitteen mitatakseen etäisyyksiä jostakin tietystä planeetasta muihin tähtiin. Oppilaat oppivat myös, miten kiertorata muuttuu. Silloin päädytään pohtimaan teoriaa: Miksi planeetalle tapahtuu noin? Onko olemassa geometristä kaavaa kiertoradan laskemiseksi? Yläkoulun viimeisiltä luokilta alkaen voidaan tähtitaivaan tarkkailu yhdistää matematiikkaan planeettojen kiertorataa koskevissa projekteissa. Matemaattisista työkaluista käytetään tässä yhteydessä mm. kartioleikkauksien laskentaa. Keplerin säännöt antavat ideoita ja perustan kiertoratojen laskemiselle.
Vihje: Simuloikaa yhdessä oppilaiden kanssa Auringon, Kuun ja muiden planeettojen liikkeitä. Aurinkoa voi simuloida esim. lampulla ja Kuuta sekä Maata kahdella erisuuruisella pallolla. Mikä näistä taivaankappaleista sijoittuu muiden väliin? Mikä näistä kiertää mitäkin ja kuinka usein? Miltä asetelma näyttää auringon- ja kuunpimennyksen aikaan? Missä kuu sijaitsee uuden kuun aikaan? Tämä koe osoittaa useimmiten, että näissä tutuissakin taivaankappaleissa on paljon opittavaa. Lue vähemmän
Vinkki - vuonna 2012 taivaalla tapahtui isoja asioita
Yksi erityinen tapahtuma tarjosi vuonna 2012 aivan erityisen syyn taivaan tarkkailuun: Venus kulki nimittäin Auringon editse 6. kesäkuuta 2012. Venus kulkee Maasta katsoen täsmälleen Auringon editse enintään kaksi ... Lue lisää
Yksi erityinen tapahtuma tarjosi vuonna 2012 aivan erityisen syyn taivaan tarkkailuun: Venus kulki nimittäin Auringon editse 6. kesäkuuta 2012. Venus kulkee Maasta katsoen täsmälleen Auringon editse enintään kaksi
kertaa vuosisadassa. Jos joku ei ylikulkua tällä kertaa nähnyt, ei hän todennäköisesti tule sitä enää kokemaan: Seuraavan Venuksen ylikulun ajankohta on nimittäin vuonna 2117. Valitettavasti Keski-Euroopassa nähdään vain osa tästä ylikulusta, sillä kun aurinko nousee 6. kesäkuuta, Venus on jo melkein kokonaan ohittanut Auringon. Ylikulkua edeltävien viikkojen aikana Venus oli kuitenkin hyvin nähtävissä yötaivaalla - mikä tarjosi hyvän syyn tarkkailla "Iltatähden" liikettä. Vuonna 2012 myös Merkurius, Jupiter ja Mars olivat myös monen viikon ajan hyvin nähtävissä tähtitaivaalla. Lue vähemmän
kertaa vuosisadassa. Jos joku ei ylikulkua tällä kertaa nähnyt, ei hän todennäköisesti tule sitä enää kokemaan: Seuraavan Venuksen ylikulun ajankohta on nimittäin vuonna 2117. Valitettavasti Keski-Euroopassa nähdään vain osa tästä ylikulusta, sillä kun aurinko nousee 6. kesäkuuta, Venus on jo melkein kokonaan ohittanut Auringon. Ylikulkua edeltävien viikkojen aikana Venus oli kuitenkin hyvin nähtävissä yötaivaalla - mikä tarjosi hyvän syyn tarkkailla "Iltatähden" liikettä. Vuonna 2012 myös Merkurius, Jupiter ja Mars olivat myös monen viikon ajan hyvin nähtävissä tähtitaivaalla. Lue vähemmän
