TEEMAOSIO

Urheilussa on monia matematiikkaa sivuavia puolia, kuten pelien säännöt ja urheiluvälineiden muoto. Poislukien muutamat urheilulajit, jossa urheilijaa arvioidaan hänen esityksensä aikaansaaman vaikutelman perusteella, kuten voimistelu ja taitoluistelu, urheilukilpailuissa tehdään koko ajan jonkinlaisia mittauksia: otetaan aikaa (juoksu), mitataan matkaa (pituushyppy, heittolajit) tai lasketaan yhteen (osumat ammunnassa, maalit jalkapallossa). Näiden mittaustulosten perusteella on helppoa verrata suorituksia ja seurata kehitystä – mittaustulokset ovat tilastolaskenan keskeistä materiaalia.

Tulos riippuu kulmasta: urheilu ja geometria

Urheiluvälineitäkin voidaan tarkastella matemaattisesti, vaikka tämä ei niistä ihan heti tulekaan mieleen. Jalkapallo ei ole tarkasti ottaen täydellisen pyöreä, vaan se koostuu usein kahdestatoista viisikulkiosta ja kahdestakymmenestä kuusikulmiosta, jotka muodostavat pyöristetyn ikosaedrin. Täten jalkapallossa ei oikeastaan pitäisi puhua ”nahkakuulasta”. Myös esimerkiksi maalintekoon liittyy geometrisiä aspekteja: Löytääkseen optimaalisen paikan laukausta varten jalkapalloilijan tulisi pyrkiä potkaisemaan pallo kohti maalia mahdollisimman suuresta kulmasta päätyrajan (nollakulma) ja sen kohdan välillä, joka on kauimpana maalista (laukaisukulma lähenee nollakulmaa).

Urheilu tilastolaskennan näkökulmasta

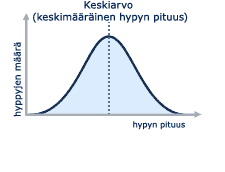
Mittaustuloksia tarkastellaan usein normaalijakauman näkökulmasta ja täten niiden odotetaan olevan keskenään riippuvaisia. Näin on asia myös urheilutulosten suhteen. Jakauma muodostuu tulosten tiheysfunktion kautta ja sen graafinen kuvaaja näyttää leveältä kellolta. Normaalijakaumaa kutsutaan myös Gaussin käyräksi tai Gaussin kellokäyräksi. Useimmat arvot sijoittuvat symmetrisesti lähelle käyrän keskikohtaa. Käyrä laskeutuu reunoja kohti ensin nopeasti ja sitten hitaammin. Ääriarvoja on hyvin vähän ja ne ovat epätodennäköisiä. Niinpä esimerkiksi 100 metrin juoksijahuiput juoksevat aikoja, jotka eroavat toisistaan vain vähän. Sekunnin kymmenykset ovat tässä lajissa suuria eroja. Keskivertosprintteri putoaisi sekunnin hitaammalla ajalla parhaisiin verrattuna käyrän ulkopuolelle.

Todelliset ja näennäiset ennätykset

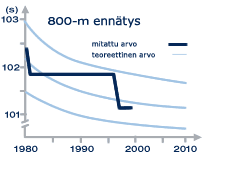
„Aina ei ole helppoa selvittää syytä ennätysten paranemiseen“, selittää Fysiikan professori Dieter Suter Dortmundista. Hän on tutkinut saksan- ja maailmanennätyksiä ja ennätysten kehittymistä eri lajeissa yhdessä Daniel Gembrisin kanssa. Tulokset osoittivat useiden lajien suoritusten jatkuvaa paranemista. Toisin sanoen, juostiin aina vaan nopeammin ja hypättiin aina vaan pitemmälle. Tilastollisesti voitiin osoittaa myös se, että sattumalla on aina silloin tällöin merkittävä rooli ennätyksissä. Juuri tämän takia urheilutapahtumat ovat myös keskeinen vedonlyönnin kohde. Mikään vedonlyöntitoimisto ei käyttäisi urheilutapahtumia vedonlyöntikohteina, jos tulokset voitaisiin ennakoida tarkasti.
„Tulokset voivat myös parantua ilman, että urheilijan suoritus paranee“, kertoo professori Suter. „Yksi syy tähän löytyy mittaustuloksista.“ Juoksulajien ennätysten selvä paraneminen johtuu muun muassa siitä, että mittaukset on voitu suorittaa entistä tarkemmin. Kun taannoin parhaiden urheilijoiden aikaerot olivat sekunnin sadasosia, nyt on yritettävä mitata aikaa sekunnin tuhannesosissa. Tulokset riippuvat siis osittain myös käytetystä mitta-asteikosta. Toisaalta monien lajien osanottajamäärät ovat kasvaneet tuntuvasti. Matematiikan näkökulmasta tarkastellen käytetyt mittayksiköt ovat siis pienentyneet. Se, että kansalliset ja kansainväliset ennätykset kehittyvät eri tahtia voi johtua yksinkertaisesti siitä, että lajien parhaat ottavat osaa pääsääntöisesti vain erityisen tärkeisiin kilpailuihin. Tästä johtuen ennätyksiä tehdään lähinnä vain kansainvälisissä kilpailuissa. Ulkoiset tekijät voivat toisaalta vaikuttaa siihen, miksi ennätyksiä tapahtuu „yllättäen“ – siis ikään kuin tilastoperusteisten odotusten vastaisesti. Tällaisia ulkoisia tekijöitä ovat mm. kilpailujen kasautuminen yhdelle vuodelle, äärimmäiset sääolosuhteet (juoksu ei suju niin hyvin kylmässä säässä). Syy voi löytyä myös urheilijan henkilökohtaisesta taktiikasta. „Ja erityisen huomattavat ennätysten parantumiset, siis sellaiset, joita ei voi tilastollisesti ennakoida, voivat viitata dopingin käyttöön “, jatkaa professori Suter.

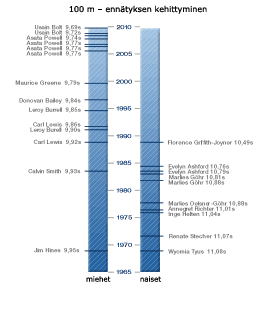
Matemaattisten mallien kanssa pitää kuitenkin olla tarkkana. On esimerkiksi todettu, että maailmanennätykset juoksulajeissa ovat kehittyneet nopeammin naisilla kuin miehillä. Molemmille ryhmille on voitu laskea suunnilleen lineaarinen kehitys. Tuloksena saatiin juostun ajan ja vuosiluvun koordinaatistossa laskevat kuvaajat. Johtuen siitä, että naisten ja miesten tulosten kehitys ei ole ollut samanlaista, oli naisten kuvaajan lasku nopeampi kuin miesten. Mikäli kehitys jatkuisi tulevaisuudessa saman tapaisena kuin kuvaajan, pitäisi kuvaajien leikata toisensa jossakin vaiheessa. Toisin sanoen, naisten tulisi tällöin saavuttaa miesten tulokset ja juosta pian nopeammin. Jossakin vaiheessa kuvaaja leikkaisi aika-akselin, mikä viimeistään paljastaisi kuvausmallin epärealistisuuden. Aika alkaisi lähentyä nollaa – tämä kuvausmalli ei ota huomioon ihmisen fyysisiä rajoituksia.

Olipa kyse ennätysten kehittymisestä 100 metrin juoksussa tai maaliin suuntautuvan laukauksen optimipaikasta – havainnolliset esimerkit urheilun maailmasta tekevät matematiikan opettamisesta ja oppimisesta mielenkiintoista. Oppilaat voivat näin tutustua matematiikan eri osa-alueisiin urheilun näkökulmasta.